Outlier Detection¶
The hdbscan library supports the GLOSH outlier detection algorithm, and does so within the HDBSCAN clustering class. The GLOSH outlier detection algorithm is related to older outlier detection methods such as LOF and LOCI. It is a fast and flexible outlier detection system, and supports a notion of local outliers. This means that it can detect outliers that may be noticeably different from points in its local region (for example points not on a local submanifold) but that are not necessarily outliers globally. So how do we find outliers? We proceed identically to the basic use of HDBSCAN*. We start with some data, and fit it with an HDBSCAN object.
plt.scatter(*data.T, s=50, linewidth=0, c='b', alpha=0.25)
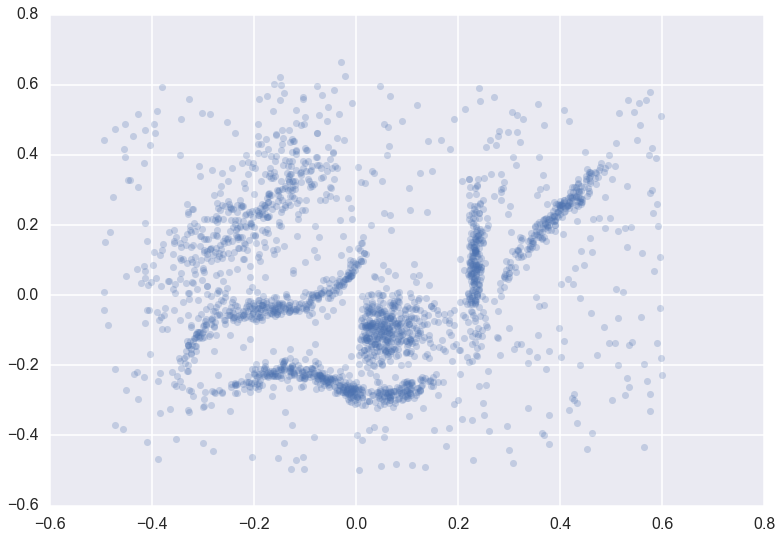
clusterer = hdbscan.HDBSCAN(min_cluster_size=15).fit(data)
The clusterer object now has an attribute (computed when first accessed)
called outlier_scores_. This provides a numpy array with a value for
each sample in the original dataset that was fit with the clusterer. The
higher the score, the more likely the point is to be an outlier. In
practice it is often best to look at the distributions of outlier
scores.
clusterer.outlier_scores_
array([ 0.14791852, 0.14116731, 0.09171929, ..., 0.62050534,
0.56749298, 0.20681685])
sns.distplot(clusterer.outlier_scores_[np.isfinite(clusterer.outlier_scores_)], rug=True)
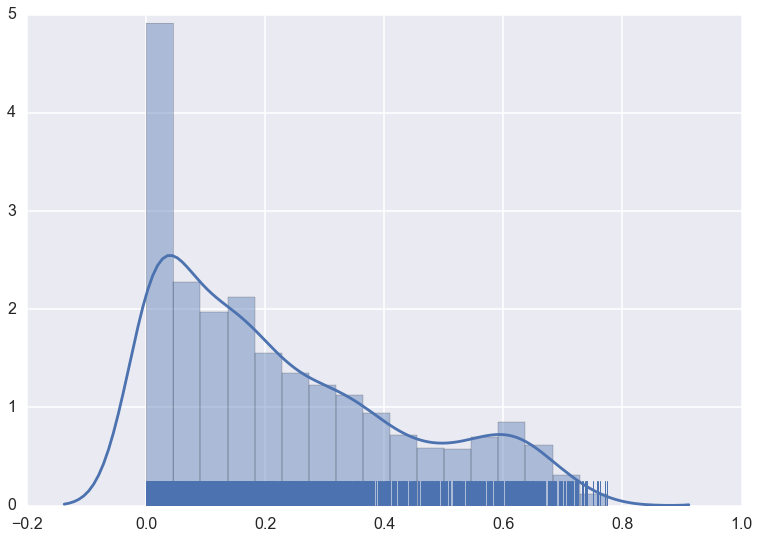
We can pull off upper quantiles to detect outliers, which we can then plot.
threshold = pd.Series(clusterer.outlier_scores_).quantile(0.9)
outliers = np.where(clusterer.outlier_scores_ > threshold)[0]
plt.scatter(*data.T, s=50, linewidth=0, c='gray', alpha=0.25)
plt.scatter(*data[outliers].T, s=50, linewidth=0, c='red', alpha=0.5)
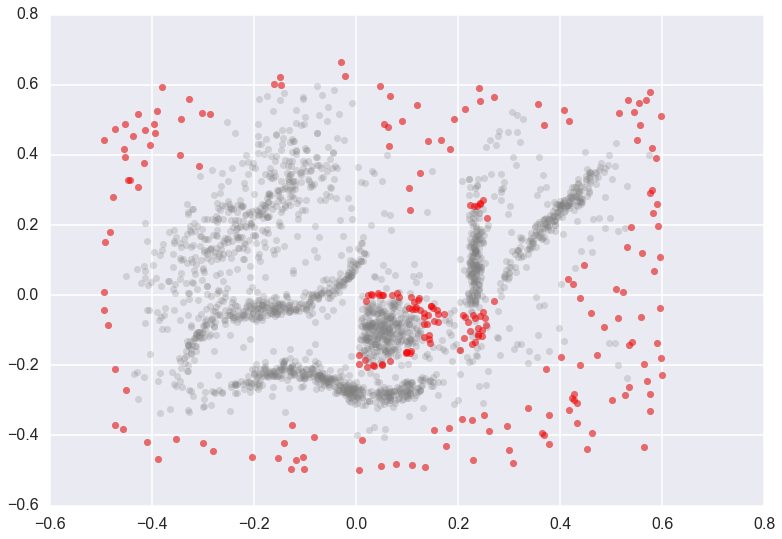
Note that not only are the outlying border points highlighted as outliers, but points at the edge of the central ball like cluster, and just below the vertical band cluster, are also designated as outliers. This is because those two clusters are extremely dense, and the points at the edge of this cluster are close enough to the cluster that they should be part of it, but far enough from the being core parts of the cluster that they are extremely unlikely and hence anomalous.